
A full discussion can be found in the book Atomic Diffusion in Stars by G. Michaud, G. Alecian & J. Richer, (2015, Astronomy and Astrophysics Library, Springer International Publishing, Switzerland).
Atomic diffusion is a physical process acting at a microscopic level. It produces macroscopic segregation of atomic species in a non-isotropic stable medium. It is a non-standard transport process because no advective term appears in the basic equations describing it.
To simplify the problem, one can say that in a star, atoms of a given species may on average be pushed upwards (towards the surface) or sink due to certain forces which are different from one species to the other (see below). Elements may then accumulate or become scarce at certain depths in the star.
This physical process, with a particularly important role of the radiative acceleration (see below), was invoked for stars by Michaud (1970) to explain abundance anomalies observed on the surface of chemically peculiar stars.
Because atomic diffusion may create significant abundance inhomogeneities outside stellar cores, it can affect the local opacities, and therefore, the structure and evolution of stars. It should, however, be noted that other physical processes such as convection, turbulence or large scale currents of matter often have a stronger effect than atomic diffusion process in many types of stars: the matter can be mixed faster than atomic diffusion separates species. Consequently, the effect of atomic diffusion is generally only important in radiative zones and for slowly rotating stars.
Even if there is no advective term in the basic equations describing atomic diffusion (obtained in the framework of kinetic theory of gases), it is possible to define a diffusion velocity for a given type of ion i (Chapman & Cowling 1970, see also discussion in Alecian 2014), which, after some approximations (plane-parallel case, test particle approximation,...), may be expressed as:
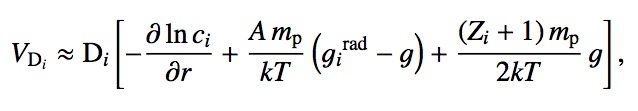
where
One may notice that the term with the spatial derivative of the concentration ci corresponds to the pure diffusion term found in hydrodynamics equations (see discussion in Alecian, 2014). The term with Zi is the contribution of the electric field (Aller & Chapman 1960). The two principal forces that are present in this expression of the diffusion velocity are the local gravity g and the radiative acceleration girad due to the momentum transfer from the radiation field to the ion i following photoexcitation or photoionization (Michaud 1970). These two accelerations have opposite signs in this algebraic expression, because g is a vector oriented towards the stellar centre while girad is a vector oriented outwards (in most cases), in the same direction as the net radiation flux (see page dedicated to radiative accelerations for more details).
Other factors also come into play where diffusion is concerned. For example, the presence of a stellar magnetic field may modify the diffusion velocity of elements in stellar atmospheres. This can lead to inhomogeneous abundance distribution over the surface of magnetic stars, related to the geometry of the magnetic field (for instance, abundance patches are detected on the surface of magnetic stars).
It should be emphasized that studies of atomic diffusion in stars are aimed in evaluating abundance distributions inside them. The processes leading to the evolution of abundance distributions are time dependent. Atomic diffusion is generally a slow process compared to other transport processes, time scales for atomic diffusion in stellar interiors may be several million years (and sometimes with the same order of magnitude as of the star's lifetime on the main-sequence). Time scales in the atmospheres are much shorter: from months to thousands of years, depending on depth. The fact that radiative accelerations depend non-linearly on the local concentrations makes the evolution of abundance distributions strongly non-linear. To overcome the numerical difficulties related to such a wide range of time scales and to the fact that the medium is optically thin (which requires detailed treatment of the radiation transfer), models for stellar atmospheres often used equilibrium solutions to estimate abundance distributions (see discussion in Alecian et. al, 2011). However, recent studies have estimated 3D time-dependent diffusion in magnetic atmospheres (Alecian & Stift, 2019).