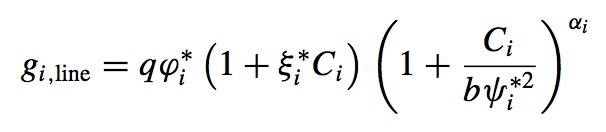

Radiative accelerations (grad), which measure the amount of momentum transferred from the radiation field to atomic species following photoexcitation or photoionization, are critical in the study of atomic diffusion in stars (Michaud 1970).
Detailed calculations of grad are numerically onerous. The SVP (standing for Single-Valued Parameters) approximation presented here makes it possible to approximate grad in stellar interiors without having to explicitly use the large amount of atomic data implicated in more detailed calculations such as those of the opacity sampling method for instance (e.g. Seaton 1997). The SVP approximation equations were specifically developed to separate the terms depending explicitly on the atomic data from those depending on the concentration of the ion. This section aims to briefly outline the SVP approximation by presenting the pertinent equations and related parameters.
For each ion considered here, six parameters are given in the tables that may be found on this web site. For grad due to bound-bound transitions, the acceleration of an ion i may be calculated with the following four parameters : φi*, ψi*, ξi* and αi (see below for the two other parameters ai and bi required for the evaluation of the acceleration due to bound-free transitions). The tables (ASCII text format) provided on this website give these parameters in columns labelled as phix_i, psix_i, xi_i and alpha_i respectively. According to the SVP method, the radiative acceleration of ion i due to its bound-bound transitions may be approximated by the following equations (see LeBlanc & Alecian 2004, and Alecian & LeBlanc, 2020):
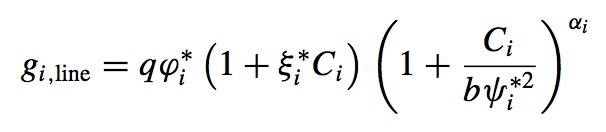
where the functions q and b (written p in Alecian & LeBlanc, 2020) are defined as follows
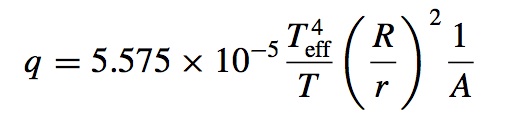
and
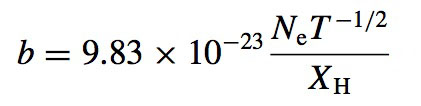
Here, Teff and R are the effective temperature (in Kelvin) and the radius of the star, while T, r and Ne are respectively the local temperature, radius and electronic density. The hydrogen mass fraction XH , the atomic number of the ion A and the concentration (in number) of the ion relative to hydrogen represented by Ci also intervene in these equations. The first three of the parameters given above are evaluated where the relative population of the ion considered is near its maximum value, while αi is determined by a fitting procedure to better reproduce saturation effects (see Alecian & LeBlanc 2002 and LeBlanc & Alecian 2004 for more details). The physical meanings of the parameters are given in these papers (see Section 2 of LeBlanc & Alecian 2004 for instance).
In the SVP approximation method, the accelerations due to bound-free transitions are estimated by the following expressions, where the two parameters ai and bi (not to be confused with the coefficient b given above) are also given in the tables that may be found on this website (defined by the columns named a_i and b_i)
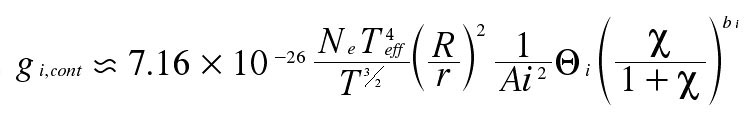
where
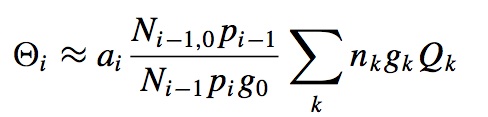
and
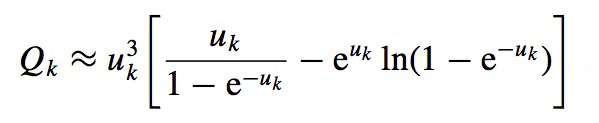
Here, Ni-1,0 is the number density of the ground level of ion A+(i-1) and Ni-1 is the number density of this ion, while the partition function of ion A+i is represented by pi . The main quantum number and the statistical weight of energy levels k of the ion A+(i-1) are represented by nk and gk. The variable u is evaluated at the ionization threshold frequency from level k where u = hν/kT. Finally χ is the abundance of the element relative to its solar value. The physical meanings of the two parameters mentioned above are found in Sections 2 and 3.2 of LeBlanc & Alecian (2004).
To evaluate the total radiative acceleration for the element A, the following weighted sum must be calculated
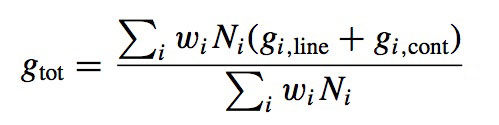
where wi is generally set to unity, unless one wants to include redistribution of momentum among the ions (e.g. Gonzalez et al. 1995). For the SVP method, Alecian & LeBlanc (2020) propose to use wi=1.5 for ions in a noble gas configuration.